Decoupling for fractal subsets of the parabola
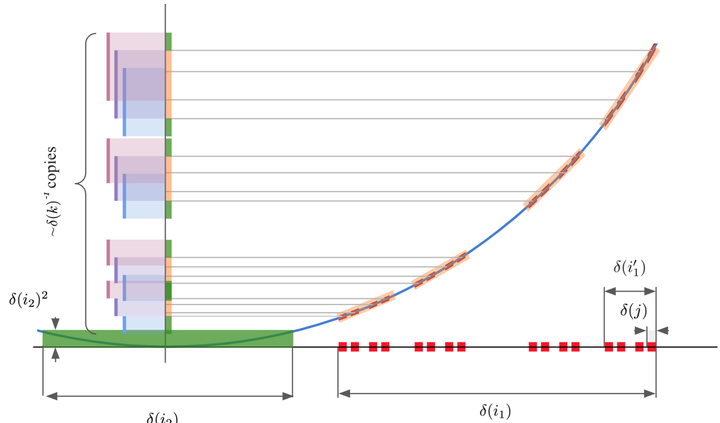 Figure from the paper
Figure from the paper
Abstract
We consider decoupling for a fractal subset of the parabola. We reduce studying l2Lp decoupling for a fractal subset on the parabola {(t,t2):0≤t≤1} to studying l2Lp/3 decoupling for the projection of this subset to the interval [0,1]. This generalizes the decoupling theorem of Bourgain-Demeter in the case of the parabola. Due to the sparsity and fractal like structure, this allows us to improve upon Bourgain-Demeter’s decoupling theorem for the parabola. In the case when p/3 is an even integer we derive theoretical and computational tools to explicitly compute the associated decoupling constant for this projection to [0,1]. Our ideas are inspired by the recent work on ellipsephic sets by Biggs using nested efficient congruencing.
Type