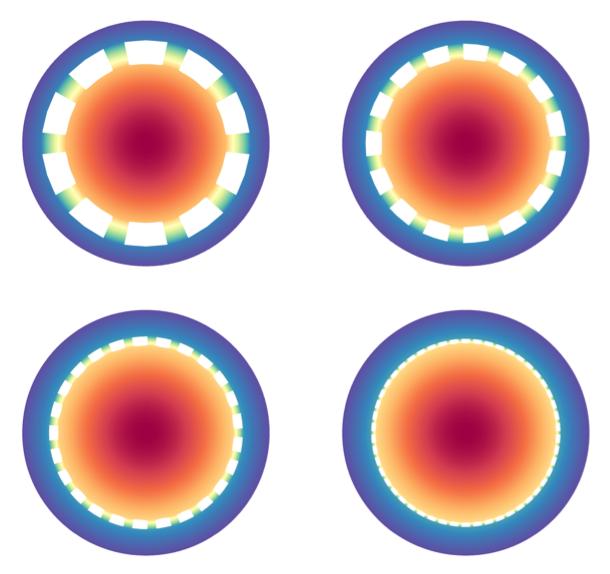
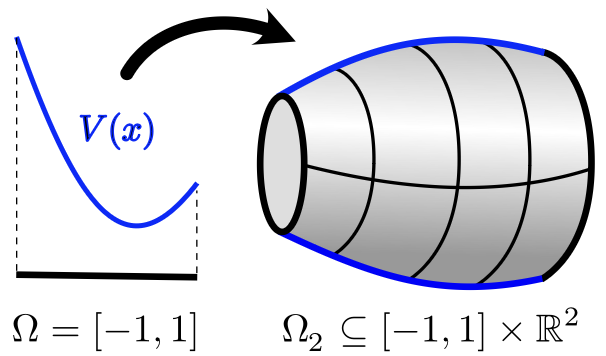
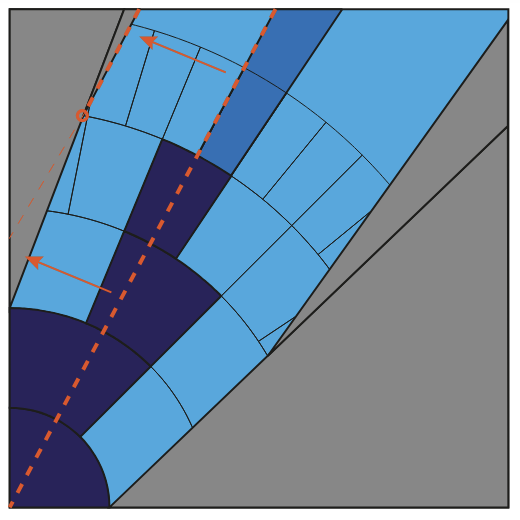
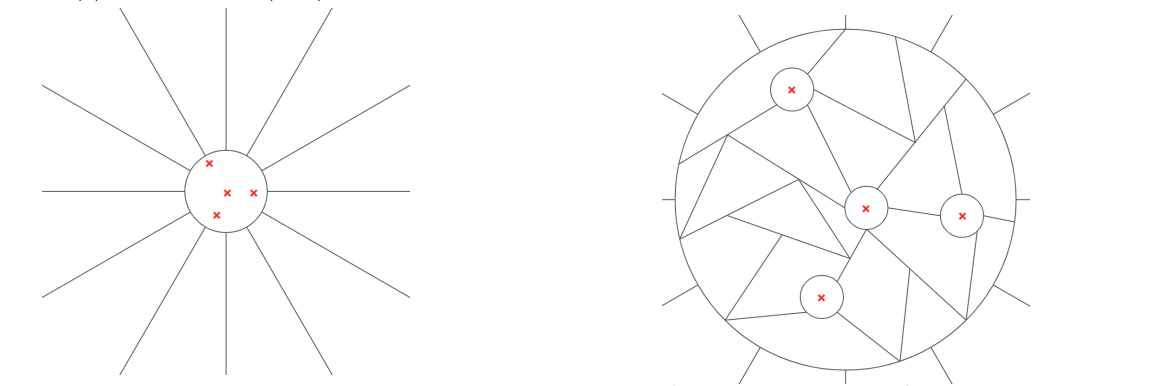
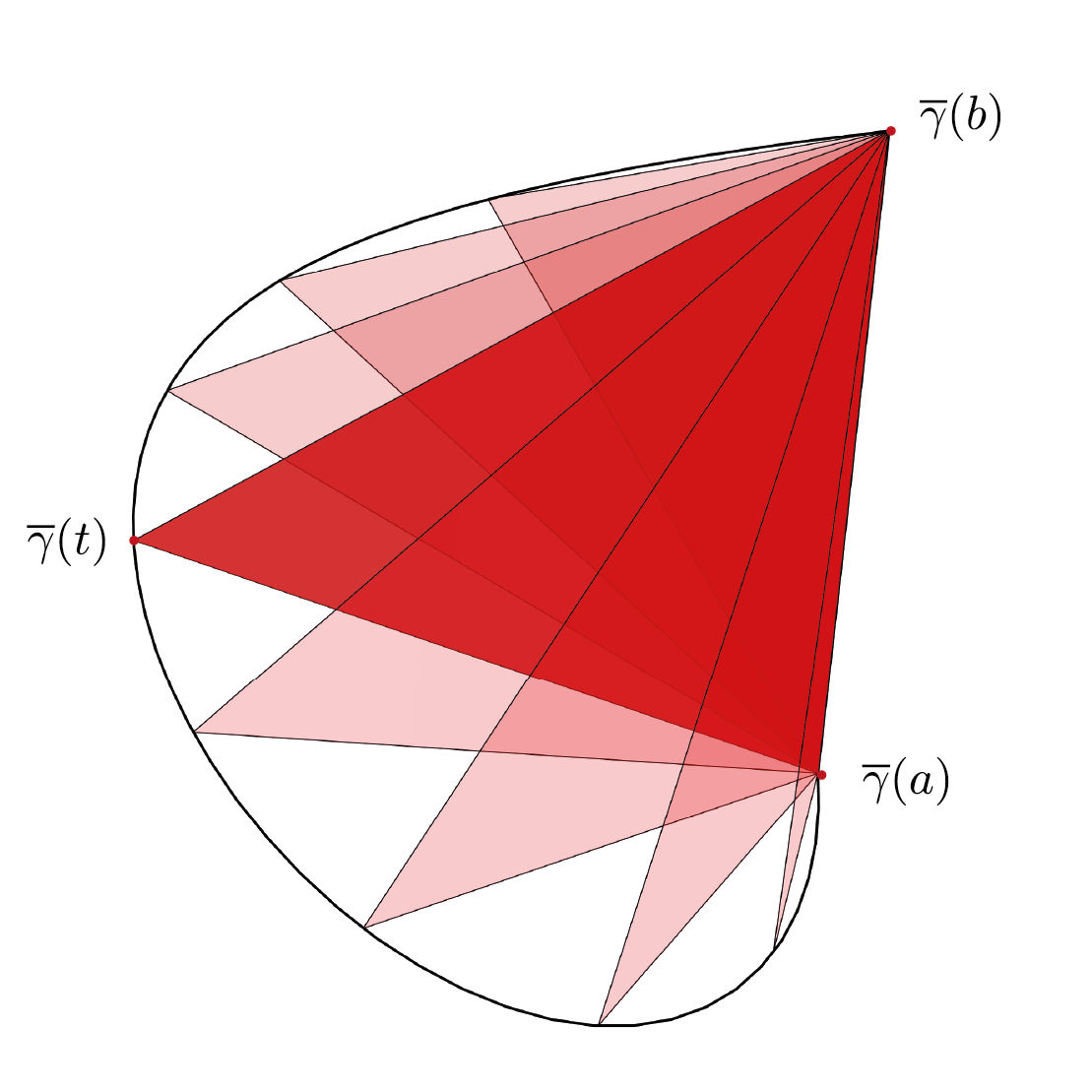
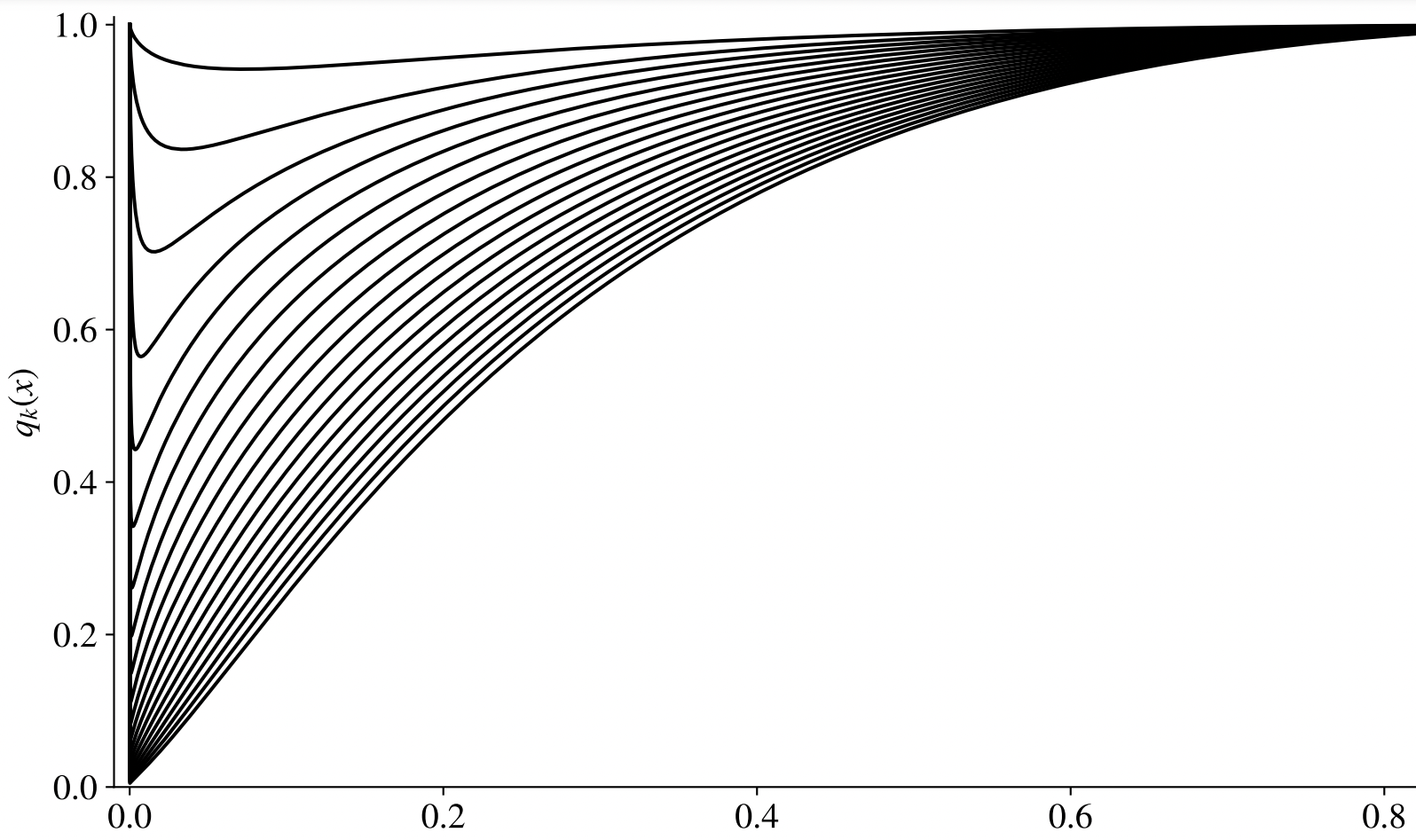
Sharp bounds on the failure of the hot spots conjecture
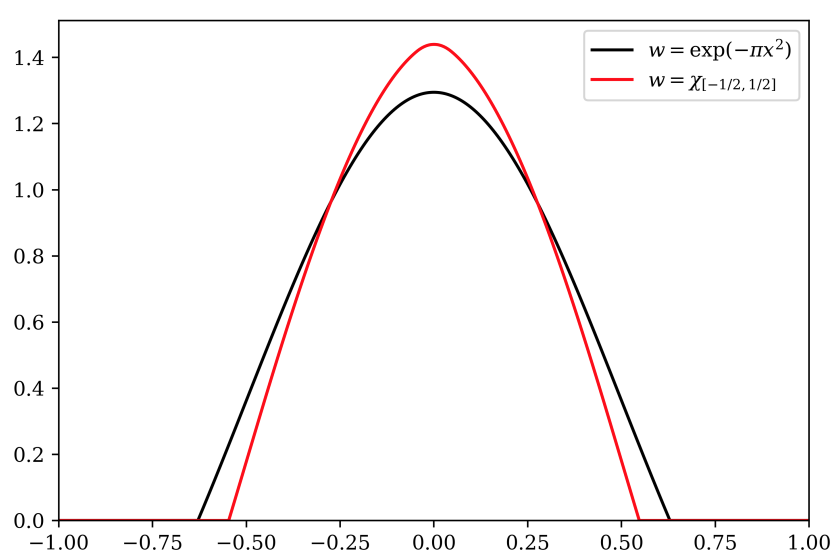
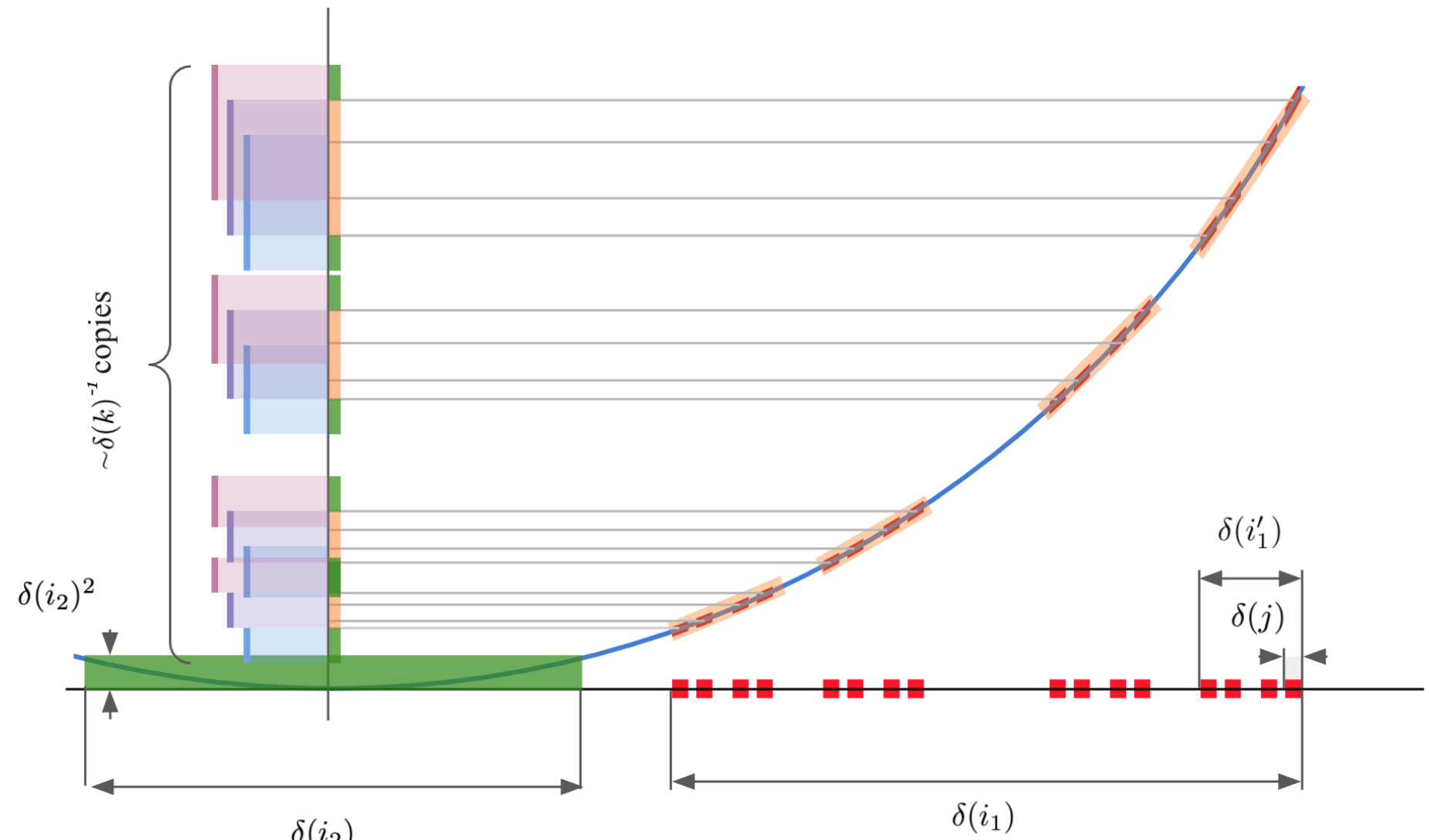
The hot spots ratio of a domain measures the degree of failure of Rauch's hot spots conjecture. We identify the largest possible value of this ratio over all connected Lipschitz domains in any dimension d. As d tends to infinity, we show that this maximal ratio converges to sqrt(e), asymptotically matching the previous best known upper bound...