Convex sets can have interior hot spots
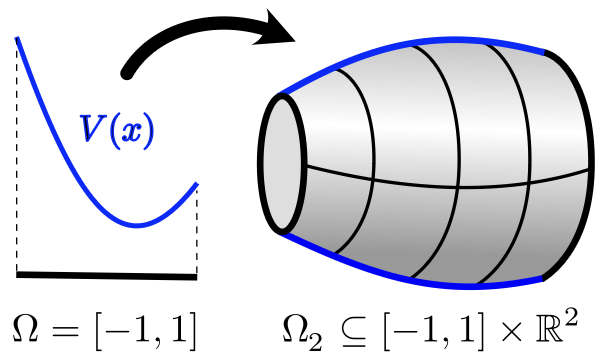 Figure from the paper
Figure from the paper
Abstract
The hot spots conjecture asserts that for any convex bounded domain $\Omega$ in $\mathbb{R}^d$, the first non-trivial Neumann eigenfunction of the Laplace operator in $\Omega$ attains its maximum at the boundary. We construct counterexamples to the conjecture for all sufficiently large values of $d$. The construction is based on an extension of the conjecture from convex sets to log-concave measures.
Type