On classical inequalities for autocorrelations and autoconvolutions
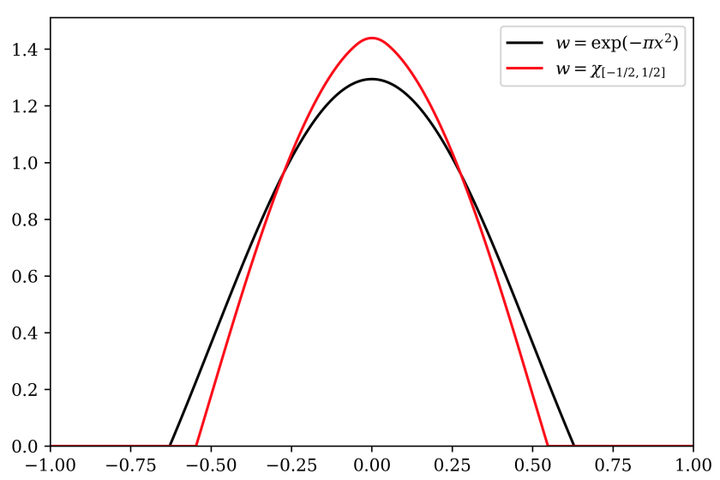 Figure from the paper
Figure from the paper
Abstract
In this paper we study an autocorrelation inequality proposed by Barnard and Steinerberger. The study of these problems is motivated by a classical problem in additive combinatorics. We establish the existence of extremizers to this inequality, for a general class of weights, including Gaussian functions (as studied by the second author and Ramos) and characteristic function (as originally studied by Barnard and Steinerberger). Moreover, via a discretization argument and numerical analysis, we find some almost optimal approximation for the best constant allowed in this inequality. We also discuss some other related problem about autoconvolutions.
Type