A new proof of the description of the convex hull of space curves with totally positive torsion
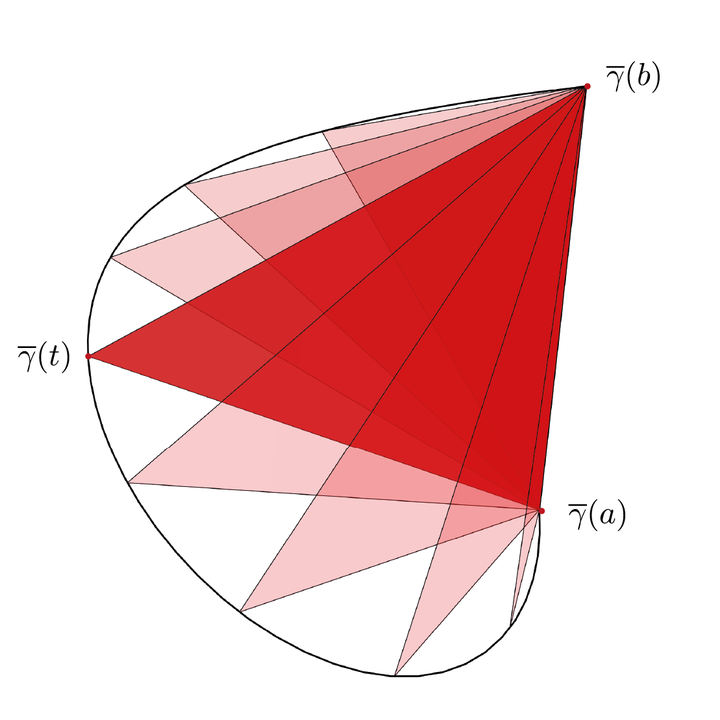 Figure from the paper
Figure from the paper
Abstract
We give new proofs of the description convex hulls of space curves $\gamma : [a,b] \mapsto \mathbb{R}^{d}$ having totally positive torsion. These are curves such that all the leading principal minors of $d\times d$ matrix $(\gamma’, \gamma’’, \ldots, \gamma^{(d)})$ are positive. In particular, we recover parametric representation of the boundary of the convex hull, different formulas for its surface area and the volume of the convex hull, and the solution to a general moment problem corresponding to $\gamma$.
Type