Periodicity and decidability of translational tilings by rational polygonal sets
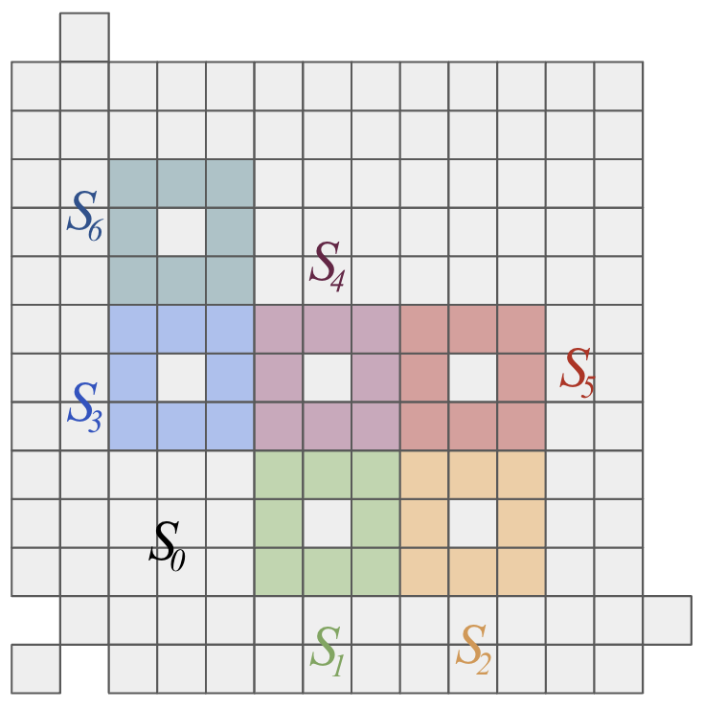 Figure from the paper
Figure from the paper
Abstract
The periodic tiling conjecture asserts that if a region Σ⊂Rd tiles Rd by translations then it admits at least one fully periodic tiling. This conjecture is known to hold in R, and recently it was disproved in sufficiently high dimensions. In this paper, we study the periodic tiling conjecture for polygonal sets: bounded open sets in R2 whose boundary is a finite union of line segments. We prove the periodic tiling conjecture for any polygonal tile whose vertices are rational. As a corollary of our argument, we also obtain the decidability of tilings by rational polygonal sets. Moreover, we prove that any translational tiling by a rational polygonal tile is weakly-periodic, i.e., can be partitioned into finitely many singly-periodic pieces.
Type